
Probabilmente a molti di noi sarà capitato, durante gli anni dell’adolescenza, di sentirsi redarguire dai genitori, con un tono un po’ seccato: «la tua stanza è un vero caos! Rimettila in ordine!» Dal che si evince che, in generale, nel linguaggio corrente, caos equivale a disordine. Ma è proprio così?
Walter J. Freeman è un neuroscienziato che coordina un’equipe di ricercatori della prestigiosa università di Berkley in California. Il team studia le applicazioni della matematica del caos ad alcuni fenomeni biologici quali, ad esempio, la previsione degli attacchi epilettici e il funzionamento del sistema olfattivo. Lo scienziato ha affermato, durante una recente conferenza:
«Il termine caos è un po’ abusato e ha troppi significati. In senso colloquiale esso significa disordine. Nella matematica si riferisce a certi comportamenti dei sistemi deterministici. Nella fisica significa rumore soggetto a vincoli. Insomma è un termine privo di base semantica. Un’accezione alternativa più utile è “dinamica non convergente”. Questa è l’espressione preferita dagli ingegneri coi quali lavoro attualmente».
Egli ci ha però fornito, in un linguaggio colloquiale, un’ottima descrizione delle differenze in realtà esistenti tra disordine e caos.
In sostanza per comprendere i due diversi fenomeni dobbiamo immaginare di assistere a due diverse condizioni. La prima descrive efficacemente il disordine. In una sala affollata qualcuno urla: «Al fuoco!» Si scatena il panico. Tutti cercano di mettersi in salvo in modo disordinato correndo laddove pensano di trovare un’uscita verso la salvezza. Non c’è, in questo caso, uno schema, una mappa mentale che guida i fuggitivi ma la manifestazione di comportamenti casuali determinati da un’emotività molto intensa. Niente potrebbe modificare questi flussi disordinati.
Ora immaginiamo invece di trovarci in un’affollatissima stazione ferroviaria: la Central Station di New York o la stazione Shinjuku di Tōkyo, frequentata quotidianamente da circa sei milioni di viaggiatori. Potremmo osservare fiumi di persone che camminano frettolosamente o corrono in direzioni diverse e, presumibilmente, ne trarremo l’impressione di assistere ad un moto disordinato, privo di un ordine o di uno schema. In realtà non è affatto così. Ogni viaggiatore sa che deve recarsi ad un determinato binario dove troverà il treno che lo porterà alla sua destinazione con un dato orario di partenza. Per noi osservatori la mancata conoscenza di queste informazioni è la causa della falsa impressione di disordine. Inoltre sappiamo che eventuali annunci di cambi di binario o di orario modificherebbero istantaneamente i flussi dei viaggiatori.
Il team del professor Freeman ha scoperto che alcune attività cerebrali hanno un andamento caotico, apparentemente casuale ma in realtà governato da logiche occulte. Ampi gruppi di cellule nervose – i neuroni – passano da uno stato complesso di attività ad un differente stato complesso in risposta a stimoli difficilmente individuabili. Caratteristica questa peculiare degli stati caotici.
Il caos è quindi un fenomeno complesso, nel quale l’indeterminatezza delle dinamiche, degli schemi e degli elementi condizionanti determina le difficoltà di interpretazione. Le fluttuazioni della Borsa, causate da eventi politici o psicologici casuali o le mutazioni meteorologiche imprevedibili sono buoni esempi di andamenti caotici. I matematici del caos usano una metafora affascinante per esprimere l’indeterminatezza meteorologica: «Il battito di una farfalla a Pechino può causare una tempesta a New York!»
Facciamo ora un salto logico e temporale. Nel 1975 un matematico polacco che aveva acquisito la cittadinanza francese, di nome Benoit Mandelbrot, si arrovellava su alcuni problemi geometrici. Mandelbrot era uno studioso del tutto sui generis. Riusciva a dimostrare complicate teorie o risolvere problemi matematici complessi grazie alla sua straordinaria capacità di trasformare le espressioni matematiche nella visione mentale di forme che sapeva rendere armoniose per poi ritrasformarle in linguaggi matematici simbolici. Nell’immediato dopoguerra superò i severissimi esami di ammissione all’ÉcoleNormale Supérieure e all’ École Polytechnique di Parigi, malgrado la sua scarsa preparazione in matematica teorica, grazie alla sua capacità di trasformare le prove di ammissione in forme visualizzate.
Nel 1975 Mandelbrot stava tentando di risolvere un problema pratico: la misurazione della lunghezza delle coste della Gran Bretagna. La soluzione gli venne offerta da un modello matematico – in realtà di geometria non euclidea – definito “fiocco di neve di Koch”. Helge von Koch (25 gennaio 1870 – 11 marzo 1924) è stato un matematico svedese che ha probabilmente disegnato il primo frattale conosciuto in un periodo nel quale il termine frattale non era stato ancora introdotto in matematica. Fu proprio Mandelbrot ad utilizzare per primo questo termine che fece derivare dal vocabolo latino fractus (rotto).
Il frattale di Koch ha un’interessante peculiarità che ha levato il sonno a molti matematici del tempo. Vediamo qui di seguito la sua descrizione.

Supponiamo che un triangolo equilatero inscritto nel cerchio abbia i tre lati lunghi 1 cm e immaginiamo di costruire su ogni lato una cuspide con due lati uguali, avente la misura pari a 1/3 del lato:
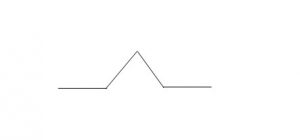
Ripetiamo ancora questa operazione – definita reiterazione – per N volte. Bene, dopo 83 reiterazioni otteniamo una figura il cui perimetro è pari alla distanza tra la terra e la luna!

In effetti si può calcolare la lunghezza del frattale moltiplicando i 3 cm (perimetro del triangolo equilatero) x 4/3 x 4/3 x 4/3 N volte. Quindi ottenere una linea la cui lunghezza è tendente all’infinito ( –> ∞). Ma ciò che levò il sonno a molti matematici del tempo fu la constatazione che una lunghezza teoricamente infinita (ogni reiterazione aumenta la lunghezza in un rapporto di 4/3) poteva essere inscritta in una superficie (il cerchio) limitata.
Un altro esempio di costruzione frattale è il cosiddetto “pulviscolo di Cantor” che, secondo Mandelbrot, che per un certo periodo si occupò di matematica pura presso l’IBM, rappresenta la distribuzione degli errori durante le trasmissioni elettroniche. Il pulviscolo venne elaborato dal matematico di origine austriaca Georg Ferdinand Ludwig Philipp Cantor (San Pietroburgo, 3 marzo 1845 – Halle, 6 gennaio 1918).

Un segmento di qualsiasi lunghezza, viene diviso in 3 parti uguali eliminando la parte centrale. Si continua procedendo nello stesso modo per N volte. Si ottiene così una “polvere” di punti il cui numero è infinito ma la cui lunghezza totale è uguale a zero. Anche il pulviscolo di Cantor, per queste sue caratteristiche che cozzavano contro la logica matematica classica, impedì il giusto riposo a molti matematici! Del resto il problema della relazione (conflittuale!) tra infinito e dimensioni finite è annoso. Il filosofo greco Zenone, vissuto nel V secolo a.C., in uno dei suoi famosi paradossi che chiamò dicotomia affermò che per percorrere una determinata distanza – ad esempio un’orgyiá (ὀργυιά, poco più di 177 cm) si deve percorrere prima metà della misura, quindi un quarto, prima ancora un ottavo e così di seguito per un numero di punti infinito. Il quesito di Zenone è quindi il seguente: come è possibile percorrere un numero infinito di posizioni in un periodo finito?
Torniamo ora, senza dare una risposta al quesito di Zenone, ai più moderni frattali. Alcuni cardiologi hanno osservato che il ritmo delle pulsazioni cardiache segue leggi frattali, probabilmente in maniera analoga alla logica del “pulviscolo di Cantor”.
I frattali si possono costruire grazie alla grafica computerizzata utilizzando una metodologia algoritmica che costruisce il modello in scala sempre più piccola. Peculiarità dei frattali è la self similarity ovvero “l’autosimilarità” condizione per la quale ogni singola parte del frattale appare molto simile all’intera figura. Forme frattali sono i fulmini, le nuvole, i cavolfiori e i polmoni che, grazie alla loro struttura frattale, riescono, in un volume molto limitato, allo scambio ossigeno/flusso ematico che richiede invece una superficie molto estesa. Il pino, che probabilmente arreda a Natale la nostra casa, è un esempio di autosimilarità. Infatti il suo tronco ha una struttura simile ai rami i quali, a loro volta, assomigliano ai rametti più piccoli, in scale via via decrescenti. Similmente la struttura di un fulmine è un frattale poiché ogni biforcazione è seguita da altre biforcazioni che hanno una struttura simile a quella di ordine superiore, ancorché di dimensioni più piccole. Mandelbrot, per rafforzare le sue affermazioni su questa logica non euclidea, affermò che i monti non sono coni e i fulmini non si propagano in linea retta!
Lo studioso applicò la logica frattale alla misurazione delle coste della Gran Bretagna. Su questo tema scrisse un famoso articolo How long is the coast of Britain? (Quanto è lunga la costa della Gran Bretagna?).
Per i lettori che, al pari del sottoscritto, sono piuttosto digiuni di scienze matematiche, sento l’obbligo di puntualizzare un importante principio: gli elementi della geometria frattale non possono essere descritti da un’equazione bensì da un algoritmo. L’algoritmo, il cui termine deriva dal nome del matematico arabo vissuto nel tredicesimo secolo Muhammad Ibn Mūsa‘l-Khwārizmī, è la descrizione analitica di una sequenza di istruzioni o di un procedimento orientato al raggiungimento di un risultato – la stesura di un programma per il computer, il programma delle lavatrici o la ricetta di una torta – mediante l’esecuzione in un determinato ordine di una serie di azioni perfettamente definite e descritte. Le proprietà dell’algoritmo sono quindi: 1) L’esistenza di un risultato ben definito da raggiungere; 2) la sequenza finita dei passi; 3) la non interpretabilità delle istruzioni (quindi l’espressione: sale q.b. non può far parte di una descrizione algoritmica); 4) l’eseguibilità delle istruzioni.
Facciamo ora un altro salto logico. Una delle straordinarie meraviglie del corpo umano riguarda la struttura del sistema neurale. Il sistema neurale è composto da cellule nervose chiamate appunto “neuroni” la cui configurazione si caratterizza per numeri da capogiro. Oggi non sappiamo esattamente quale sia il numero totale di neuroni ospitato dal corpo umano, data l’ovvia difficoltà di conteggio. Sembra comunque che si aggiri all’interno di un intervallo numerico compreso tra i 30 e i 100 miliardi!
I neuroni – che possono raggiungere la lunghezza di tutto il corpo umano, quindi all’incirca 170 – 180 cm – sono muniti di propaggini definite assoni e dentriti i quali si sfiorano per realizzare quel fenomeno biologico definito “sinapsi”, vale a dire il collegamento anatomico che consente lo scambio di pacchetti elettrochimici. Per realizzare questo fenomeno, che permette all’essere umano di muoversi, di pensare, di agire il sistema neurale si organizza in plessi o aggregazioni di cellule che interagiscono tra di loro. Per dare un’idea della complessità e dei numeri del sistema basti pensare che nel corpo di un bambino all’età di 3 anni sono presenti ben dieci trilioni di connessioni sinaptiche!
Il sistema reticolare di neuroni, assoni e dentriti quindi è ramificato secondo una logica frattale grazie alle sue dimensioni tendenti all’infinito situate in strutture corporee limitate.
I matematici del caos affermano che l’instabilità tipica degli stati caotici, che è servita per studiare ad esempio la dinamica dei fluidi, i ritmi della caduta dell’acqua da un rubinetto gocciolante, servirà anche ad approfondire lo studio della fisiologia umana, in un’ottica che completa gli approcci più ortodossi. Inoltre l’osservazione dell’attività nervosa neurale della corteccia cerebrale ha dimostrato un’alternanza di “raffiche” di impulsi, dalla quiete all’iperattività, inspiegabile secondo una logica periodica lineare.
Benoit Mandelbrot ha scritto: «Si ritiene che in qualche modo i frattali abbiano delle corrispondenze con la struttura della mente umana, è per questo che la gente li trova così familiari. Questa familiarità è ancora un mistero e più si approfondisce l’argomento più il mistero aumenta».
Mandelbrot sosteneva infatti, dimostrando e applicando matematicamente il principio della autosimilarità, che gli oggetti della natura hanno una struttura tipica della geometria frattale mentre le figure della geometria euclidea – sfere, cerchi, rette, triangoli – appartengono al mondo della speculazione slegato dalla realtà. La Natura sarebbe quindi un insieme complesso di forme frattali!
Analogamente il nostro sistema neurale, che ci permette di pensare, agire, comunicare, provare emozioni, con le sue enormi dimensioni possiede una struttura frattale! Ogni neurone influenza sinapticamente, grazie allo scambio elettrochimico tra assoni e dentriti, da diecimila a cinquantamila altri neuroni: immaginate quindi quali e quante connessioni e scambi elettrrochimici intervengono durante la normale attività neurale dell’uomo. Se pensiamo alle possibili connessioni ed interazioni tra neuroni arriviamo a numeri tendenti all’infinito che disegnano scenari di complessità frattale.
Tutto questo, come sostenuto da Mandelbrot, non può non avere effetti sulla psicologia umana e segnatamente sul senso estetico umano. Guardiamo ammirati gli alberi secolari, un paesaggio nuvoloso o le coste di un’isola grazie a similitudini anatomiche strutturali. La nostra configurazione neurale ci ricorda – inconsciamente – le molteplici forme della natura!
Per questo motivo generalmente preferiamo alle forme della geometria euclidea – rette, punti, circonferenze – i paesaggi montani, gli alberi, un panorama battuto dal vento od un cielo solcato da nuvole nere, tutte forme estranee alla geometria euclidea e questa propensione sarebbe determinata dal fatto che i nostri sistemi anatomici e neurali hanno un’analoga logica frattale. Quindi è questa somiglianza strutturale, questa affinità tra le forme degli oggetti naturali che popolano il mondo fisico e le configurazioni interne del nostro corpo, che determinerebbe in larga misura il senso estetico dell’uomo.
Gli psicologi affermano che alcune forme di oggetti o di architetture ci sono familiari o gradite a causa di analogie anatomiche che talvolta vengono percepite solo con modalità subliminali. L’architettura degli antichi era costellata di obelischi, la cui struttura fallica è evidente. L’estetica greca era ossessionata dalla sectio aurea. Sezione che fa parte della logica dell’universo, dell’armonia musicale e di quella matematica.
L’essere umano vive grazie a numerose attività biologiche in gran parte incontrollate: respirazione, circolazione ematica, battito cardiaco e attività cerebrali complesse. Il nostro corpo quindi e gran parte delle sue funzioni biologiche è dominato da attività caotiche che non percepiamo ma che condizionano il nostro stare al mondo.




